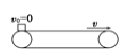
情景 | 傳送帶類別 | 圖示 | 滑塊可能的運動情況 | 滑塊受(摩擦)力分析 |
情景1 | 水平 |
| 一直加速 | 受力f=μmg |
先加速后勻速 | 先受力f=μmg,后f=0 | |||
情景2 | 水平 |
| v0>v,一直減速 | 受力f=μmg |
v0>v,先減速再勻速 | 先受力f=μmg,后f=0 | |||
v0<v,一直加速 | 受力f=μmg | |||
v0<v,先加速再勻速 | 先受力f=μmg,后f=0 | |||
情景3 | 水平 |
| 傳送帶長度l< | 受力f=μmg(方向一直向右) |
傳送帶長度l≥ | 受力f=μmg(方向一直向右) | |||
傳送帶長度l≥ | 減速和反向加速時受力f=μmg(方向一直向右),勻速運動f=0 | |||
情景4 | 傾斜 |
| 一直加速 | 受摩擦力f=μmgcosθ |
先加速后勻速 | 先受摩擦力f=μmgcosθ,后f=mgsinθ | |||
情景5 | 傾斜 |
| 一直加速 | 受摩擦力f=μmgcosθ |
先加速后勻速 | 先受摩擦力f=μmgcosθ,后f=mgsinθ | |||
先以加速度a1加速,后以加速度a2加速 | 先受摩擦力f=μmgcosθ,后受反向的摩擦力f=μmgcosθ | |||
情景6 | 傾斜 |
| 一直加速 | 受摩擦力f=μmgcosθ |
先加速后勻速 | 先受摩擦力f=μmgcosθ,后f=mgsinθ | |||
一直勻速(v0>v) | 受摩擦力f=mgsinθ | |||
一直勻速(v0=v) | 受摩擦力f=0 | |||
先以加速度a1加速,后以加速度a2加速 | 先受摩擦力f=μmgcosθ,后受反向的摩擦力f=μmgcosθ | |||
情景7 | 傾斜 |
| 一直加速 | 受摩擦力f=μmgcosθ |
一直勻速 | 受摩擦力f=mgsinθ | |||
先減速后反向加速 | 受摩擦力f=μmgcosθ, |
【例1】如圖1所示,一水平傳送裝置由輪半徑均為R的主動輪O1和從動輪O2及傳送帶等構成。兩輪軸心相距8.0 m,輪與傳送帶不打滑。現用此裝置運送一袋面粉,已知這袋面粉與傳送帶之間的動摩擦因數為μ=0.4。(g取10 m/s2)求

(1)當傳送帶以4.0 m/s的速度勻速運動時,將這袋面粉由左端O2正上方的A點輕放在傳送帶上后(設面粉初速度近似為零),這袋面粉由A端運送到O1正上方的B端所用的時間為多少?
(2)要想盡快將面粉由A端送到B端,主動輪O1的轉速至少應為多大?
【解析】設這袋面粉質量為m,其在與傳送帶產生相對滑動的過程中所受摩擦力f=μmg。故其加速度為a==μg=4.0 m/s2。
(1)若傳送帶的速度v帶=4.0 m/s,則這袋面粉加速運動的時間t1=v帶/a=1.0 s,在t1時間內的位移x1為x1=at12=2.0 m。
其后以v=4.0 m/s的速度做勻速運動,
x2=lAB-x1=vt2,
解得:t2=1.5 s。
運動的總時間為:t=t1+t2=2.5 s。
(2)要想時間最短,這袋面粉應一直向B端做加速運動,由lAB=at′2可得t′=2.0 s。
面粉到達B端時的速度v′=at′=8.0 m/s,即傳送帶運轉的最小速度。
由v′=ωR=2πnR可得:n=?r/min。
【例2】如圖2所示,質量為m的物體從離傳送帶高為H處沿光滑圓弧軌道下滑,水平滑上長為L的靜止的傳送帶并落在水平地面的Q點,已知物體與傳送帶間的動摩擦因數為μ,則當傳送帶轉動時,物體仍以上述方式滑下,將落在Q點的左邊還是右邊 ?

【解析】物體從P點滑下,設水平滑上傳送帶時的速度為v0,則由機械能守恒mgH=mv02,可得。
當傳送帶靜止時,分析物體在傳送帶上的受力知物體做勻減速運動,a=μmg/m=μg。物體離開傳送帶時的速度為,隨后做平拋運動而落在Q點。當傳送帶逆時針方向轉動時,分析物體在傳送帶上的受力情況與傳送帶靜止時相同,因而物體離開傳送帶時的速度仍為,隨后做平拋運動而仍落在Q點。(當v02<2μgL時,物體將不能滑出傳送帶而被傳送帶送回,顯然不符合題意)
當傳送帶順時針轉動時,可能出現五種情況:
(1)當傳送帶的速度v較小,時,分析物體在傳送帶上的受力可知,物體一直做勻減速運動,離開傳送帶時的速度為,因而仍將落在Q點。
(2)當傳送帶的速度![]() 時,分析物體在傳送帶上的受力可知,物體將在傳送帶上先做勻減速運動,后做勻速運動,離開傳送帶時的速度
時,分析物體在傳送帶上的受力可知,物體將在傳送帶上先做勻減速運動,后做勻速運動,離開傳送帶時的速度![]() ,因而將落在Q點的右邊。
,因而將落在Q點的右邊。
(3)當傳送帶的速度![]() =v0時,則物體在傳送帶上不受摩擦力的作用而做勻速運動,離開傳送帶時的速度
=v0時,則物體在傳送帶上不受摩擦力的作用而做勻速運動,離開傳送帶時的速度![]() ,因而將落在Q點的右邊。
,因而將落在Q點的右邊。
(4)當傳送帶的速度![]() 時,分析物體在傳送帶上的受力可知,物體將在傳送帶上先做勻加速運動,后做勻速運動,離開傳送帶時的速度
時,分析物體在傳送帶上的受力可知,物體將在傳送帶上先做勻加速運動,后做勻速運動,離開傳送帶時的速度![]() ,因而將落在Q點的右邊。
,因而將落在Q點的右邊。
(5)當傳送帶的速度v較大 ![]() 時,分析物體在傳送帶上的受力可知,物體一直做勻加速運動,離開傳送帶時的速度為
時,分析物體在傳送帶上的受力可知,物體一直做勻加速運動,離開傳送帶時的速度為![]() ,因而將落在Q點的右邊。
,因而將落在Q點的右邊。
綜上所述:
當傳送帶逆時針轉動或順時針轉動且速度![]() 時,物體仍將落在Q點;
時,物體仍將落在Q點;
當傳送帶順時針轉動且速度![]() 時,物體將落在Q點的右邊。
時,物體將落在Q點的右邊。
【例3】如圖3所示,繃緊的傳送帶,始終以2 m/s的速度勻速斜向上運行,傳送帶與水平方向間的夾角θ=30°。現把質量為10 kg的工件輕輕地放在傳送帶底端P處,由傳送帶傳送至頂端Q處。已知P、Q之間的距離為4 m,工件與傳送帶間的動摩擦因數為μ=![]() ,取g=10 m/s2。求:
,取g=10 m/s2。求:

(1)通過計算說明工件在傳送帶上做什么運動;
(2)求工件從P點運動到Q點所用的時間。
【解析】(1)對工件進行受力分析,由牛頓第二定律得:
μmgcosθ-mgsinθ=ma,
代入數值得:a=2.5 m/s2。
則其速度達到傳送帶速度時發生的位移為x1=![]() =0.8 m<4 m。
=0.8 m<4 m。
可見工件先勻加速運動0.8 m,然后勻速運動3.2 m。
(2)勻加速時,由x1=![]() t1得t1=0.8 s,
t1得t1=0.8 s,
勻速上升時t2=![]() =1.6 s,
=1.6 s,
所以工件從P點運動到Q點所用的時間為t=t1+t2=2.4 s。
【例4】如圖4所示,傳送帶與水平面夾角為37°,并以v=10m/s運行,在傳送帶的A端輕輕放一個小物體,物體與傳送帶之間的動摩擦因數μ=0.5,AB長16 m,求:以下兩種情況下物體從A到B所用的時間。

(1)傳送帶順時針方向轉動;
(2)傳送帶逆時針方向轉動。
【解析】(1)傳送帶順時針方向轉動時受力如圖4-1,由牛頓第二定律得

mgsinθ-μmgcosθ=ma,
物體下滑的加速度為a=gsinθ-μgcosθ=2m/s2。
加速的位移為s=![]() at2,故有加速的時間為:
at2,故有加速的時間為:![]() 。
。
(2)傳送帶逆時針方向轉動物體受力如圖4-2,開始摩擦力方向向下,向下勻加速運動。

a=gsin37°+μgcos37°=10m/s2,
加速的時間為t1=v/a=1s。
加速的位移為s1=![]() at2 =5m,
at2 =5m,
還剩位移s2=11m。
由題意,1s后,速度達到10m/s,摩擦力方向變為向上,由牛頓第二定律得
a2=g sin37°-μg cos37°=2 m/s2。
由運動學公式得s2=vt2+![]() a2t22,解得t2=1s,
a2t22,解得t2=1s,
故從A點到B點的時間為t=t1+t2=2s。
在水平方向的傳送帶問題中物塊的受力主要是討論滑動摩擦力,在存在相對運動時就會存在摩擦力,因此分析問題時以滑塊是否與傳送帶共速為臨界進行分析討論。
在斜面方向上的傳送帶問題中物塊的受力就要復雜些了,物體相對傳送帶滑動或者有滑動的趨勢是判斷摩擦力方向的關鍵,比如滑塊受到沿斜面向下的滑動摩擦力作用,這樣物體在沿斜面方向上所受的合力為重力的下滑分力和向下的滑動摩擦力,物體要做勻加速運動。當物體加速到與傳送帶有相同速度時,摩擦力情況要發生變化,同速的瞬間可以看成二者間相對靜止,無滑動摩擦力,但物體此時還受到重力的下滑分力作用,因此相對于傳送帶有向下的運動趨勢。若重力的下滑分力大于物體和傳送帶之間的最大靜摩擦力,此時有μ<tanθ,則物體將向下加速,所受摩擦力為沿斜面向上的滑動摩擦力;若重力的下滑分力小于或等于物體和傳送帶之間的最大靜摩擦力,此時有μ≥tanθ,則物體將和傳送帶相對靜止一起向下勻速運動,所受靜摩擦力沿斜面向上,大小等于重力的下滑分力。也可能出現的情況是傳送帶比較短,物體還沒有加速到與傳送帶同速就已經滑到了底端,這樣物體全過程都是受沿斜面向上的滑動摩擦力作用。